Simplifying Fractions

Definition: Simplifying a fraction means making the numbers smaller but keeping the fraction's value the same. You find a number that works for both the top and bottom, divide them, and the fraction becomes easier to use while still meaning the same thing

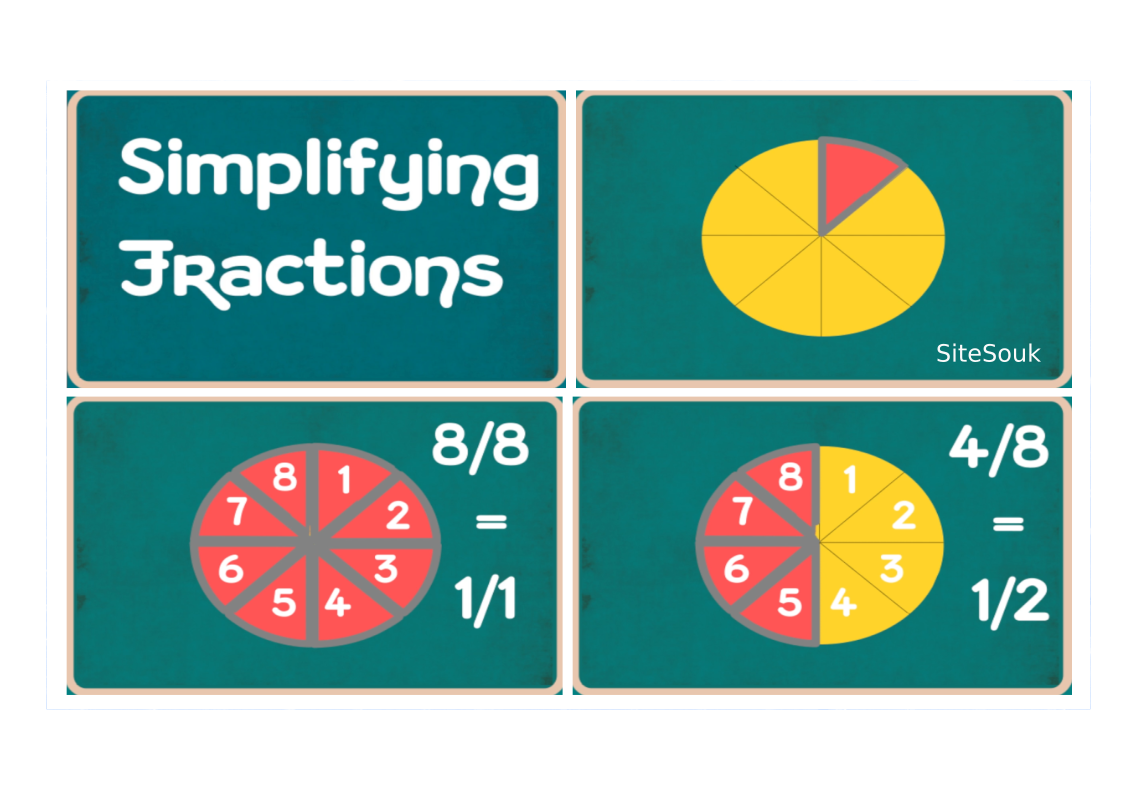
Example:

When simplifying fractions, the goal is to express the fraction in its simplest form, where the numerator and denominator have no common factors other than 1. This makes it easier to work with the fraction in equations or everyday problems. Let's walk through how to simplify the fraction 4/8 step by step:

Simplifying Fractions: A Step-by-Step Process

A fraction like 4/8 can be simplified by finding the greatest common factor (GCF) of both the numerator and the denominator. Here's how you can do it:

1. Identify the Numerator and Denominator

In this case:

• The numerator is the top number: 4.
• The denominator is the bottom number: 8.

2. Find the Factors of the Numerator

The factors are the numbers that divide the numerator evenly. For 4, the factors are:
1, 2, 4.

3. Find the Factors of the Denominator

Similarly, list the numbers that divide the denominator 8 evenly. The factors of 8 are:
1, 2, 4, 8.

4. Determine the Greatest Common Factor (GCF)

To simplify the fraction, find the largest number that is a factor of both the numerator and denominator.

• The common factors of 4 and 8 are (1, 2, 4).
• The greatest common factor (GCF) is (4).

5. Divide the Numerator and Denominator by the GCF

Now that we know the GCF, divide both the numerator and the denominator by this value:

• Divide (4 \ 4 = 1) for the numerator.
• Divide (8 \ 4 = 2) for the denominator.

Final Answer:

4/8 simplifies to 1/2.

By reducing the fraction, we've simplified 4/8 to its lowest terms: 1/2. This process can be applied to any fraction to make it simpler and more manageable.

Example 2: 6/12​

1. Find the GCF: The greatest common factor of 6 and 12 is 6.
2. Divide:
   • Top: 6 ÷ 6 = 1
   • Bottom: 12 ÷ 6 = 2
3. Simplified Fraction: 6/12 = 1/2​

Example 3: 8/16

1. Find the GCF: The greatest common factor of 8 and 16 is 8.
2. Divide:
   • Top: 8 ÷ 8 = 1
   • Bottom: 16 ÷ 8 = 2
3. Simplified Fraction: 8/16 = 1/2​

Example 4: 10/15​

1. Find the GCF: The greatest common factor of 10 and 15 is 5.
2. Divide:
   • Top: 10 ÷ 5 = 2
   • Bottom: 15 ÷ 5 = 3
3. Simplified Fraction: 10/15 = 2/3​

Example 5: 12/16​

1. Find the GCF: The greatest common factor of 12 and 16 is 4.
2. Divide:
   • Top: 12 ÷ 4 = 3
   • Bottom: 16 ÷ 4 = 4
3. Simplified Fraction: 12/16=3/4​

Example 6: 9/27​

1. Find the GCF: The greatest common factor of 9 and 27 is 9.
2. Divide:
   • Top: 9 ÷ 9 = 1
   • Bottom: 27 ÷ 9 = 3
3. Simplified Fraction: 9/27=1/3​

These examples show how to simplify fractions by finding the greatest common factor and dividing both the numerator and denominator by that number.